Soalan 7:
Rajah 4 menunjukkan bacaan jam randik mekanikal pada awal dan akhir suatu eksperimen. Jam randik ini digunakan untuk mengukur masa 20 ayunan lengkap suatu bandul ringkas yang panjangnya, l.
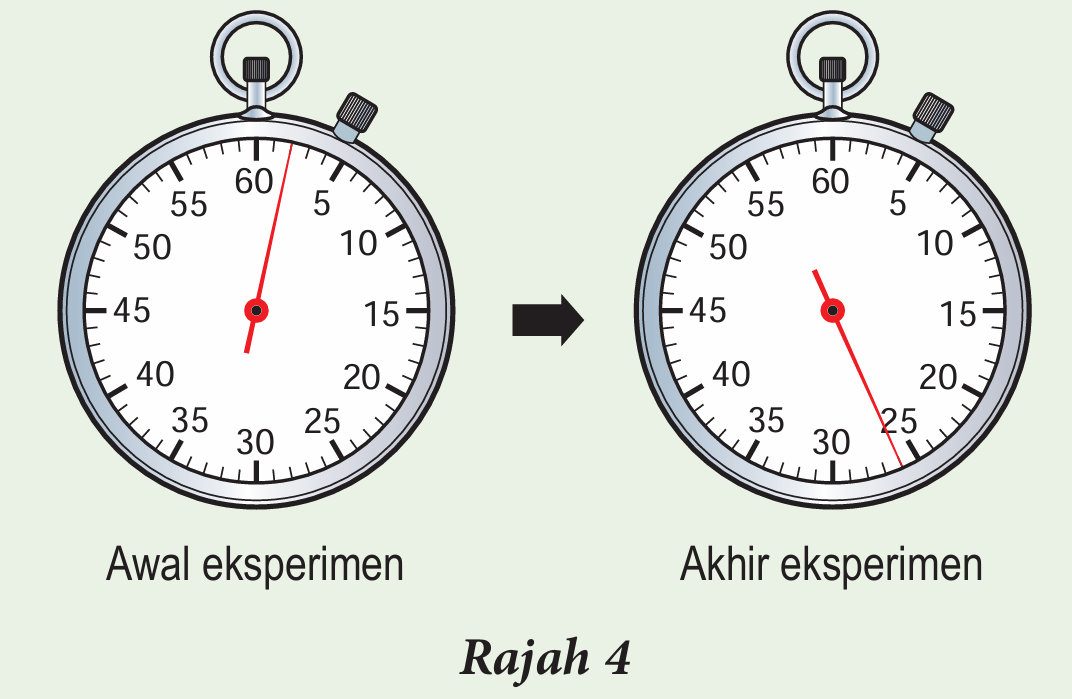
(a) (i) Berapakah masa yang diambil untuk bandul itu melengkapkan 20 ayunan?
(ii) Mengapakah masa untuk 20 ayunan lengkap perlu diambil?
(iii) Cadangkan dua langkah penambahbaikan untuk eksperimen ini.
(b)(i) Tentukan tempoh ayunan lengkap, T, bagi bandul ini.
(ii) Hubungan antara panjang, l, dan tempoh, T, suatu bandul ringkas diberikan melalui persamaan, l = (g/4π2)T2.
Dengan menggunakan nilai T dalam (b)(i), hitungkan panjang bandul, l itu.
[g = 10 m s–2]
Jawapan:
(a)(i) 26 – 2 = 24 s
(a)(ii) Untuk mendapatkan nilai satu ayunan yang lengkap dengan tepat.
(a)(iii) Langkah 1: Ulangi eksperimen dan dapatkan nilai purata dua set bacaan tersebut.
Langkah 2: Gunakan jam randik elektronik atau digital untuk mengukur masa dengan lebih tepat.
(b)(i)
$$ \text { Tempoh } T=\frac{24}{20}=1.2 \mathrm{~s} $$
(b)(ii)
$$ \begin{aligned} l & =10 \div\left(4 \times \pi^2\right) \times 1.2^2 \\ & =0.36 \mathrm{~m} \end{aligned} $$
Rajah 4 menunjukkan bacaan jam randik mekanikal pada awal dan akhir suatu eksperimen. Jam randik ini digunakan untuk mengukur masa 20 ayunan lengkap suatu bandul ringkas yang panjangnya, l.

(a) (i) Berapakah masa yang diambil untuk bandul itu melengkapkan 20 ayunan?
(ii) Mengapakah masa untuk 20 ayunan lengkap perlu diambil?
(iii) Cadangkan dua langkah penambahbaikan untuk eksperimen ini.
(b)(i) Tentukan tempoh ayunan lengkap, T, bagi bandul ini.
(ii) Hubungan antara panjang, l, dan tempoh, T, suatu bandul ringkas diberikan melalui persamaan, l = (g/4π2)T2.
Dengan menggunakan nilai T dalam (b)(i), hitungkan panjang bandul, l itu.
[g = 10 m s–2]
Jawapan:
(a)(i) 26 – 2 = 24 s
(a)(ii) Untuk mendapatkan nilai satu ayunan yang lengkap dengan tepat.
(a)(iii) Langkah 1: Ulangi eksperimen dan dapatkan nilai purata dua set bacaan tersebut.
Langkah 2: Gunakan jam randik elektronik atau digital untuk mengukur masa dengan lebih tepat.
(b)(i)
$$ \text { Tempoh } T=\frac{24}{20}=1.2 \mathrm{~s} $$
(b)(ii)
$$ \begin{aligned} l & =10 \div\left(4 \times \pi^2\right) \times 1.2^2 \\ & =0.36 \mathrm{~m} \end{aligned} $$
Soalan 8:
Hukum Kegravitian Semesta Newton boleh dinyatakan dalam bentuk persamaan berikut:
$$ F=\frac{G M m}{r^2} $$

(a) Berdasarkan persamaan tersebut, nyatakan satu contoh
(i) kuantiti asas
(ii) kuantiti terbitan, dan
(iii) kuantiti vektor.
(b) Terbitkan unit G dalam sebutan unit asas S.I.
Jawapan:
(a)(i) Kuantiti asas – Jisim, jarak, panjang
(a)(ii) Kuantiti terbitan – Daya
(a)(iii) Kuantiti vektor – Daya
(b)
$$ \text { Unit S.I. bagi } G=\frac{F r^2}{M m} $$$$ \begin{aligned} & =\frac{\mathrm{kg} \mathrm{~m} \times \mathrm{m}^2}{\mathrm{~s} \times \mathrm{s} \times \mathrm{kg} \times \mathrm{kg}} \\ & =\mathrm{kg}^{-1} \mathrm{~m}^3 \mathrm{~s}^{-2} \end{aligned} $$
Hukum Kegravitian Semesta Newton boleh dinyatakan dalam bentuk persamaan berikut:
$$ F=\frac{G M m}{r^2} $$

(a) Berdasarkan persamaan tersebut, nyatakan satu contoh
(i) kuantiti asas
(ii) kuantiti terbitan, dan
(iii) kuantiti vektor.
(b) Terbitkan unit G dalam sebutan unit asas S.I.
Jawapan:
(a)(i) Kuantiti asas – Jisim, jarak, panjang
(a)(ii) Kuantiti terbitan – Daya
(a)(iii) Kuantiti vektor – Daya
(b)
$$ \text { Unit S.I. bagi } G=\frac{F r^2}{M m} $$$$ \begin{aligned} & =\frac{\mathrm{kg} \mathrm{~m} \times \mathrm{m}^2}{\mathrm{~s} \times \mathrm{s} \times \mathrm{kg} \times \mathrm{kg}} \\ & =\mathrm{kg}^{-1} \mathrm{~m}^3 \mathrm{~s}^{-2} \end{aligned} $$
Soalan 9:
Seorang pemandu ingin tahu penggunaan petrol oleh enjin kereta bagi setiap 1 km untuk perjalanan sejauh 300 km pada kelajuan malar. Beliau memasang alat pengukur isi padu petrol dalam keretanya untuk mencatatkan bacaan baki isi padu petrol pada setiap jarak 50 km dari titik permulaan. Jadual 4 menunjukkan bacaan-bacaan yang diperolehnya.
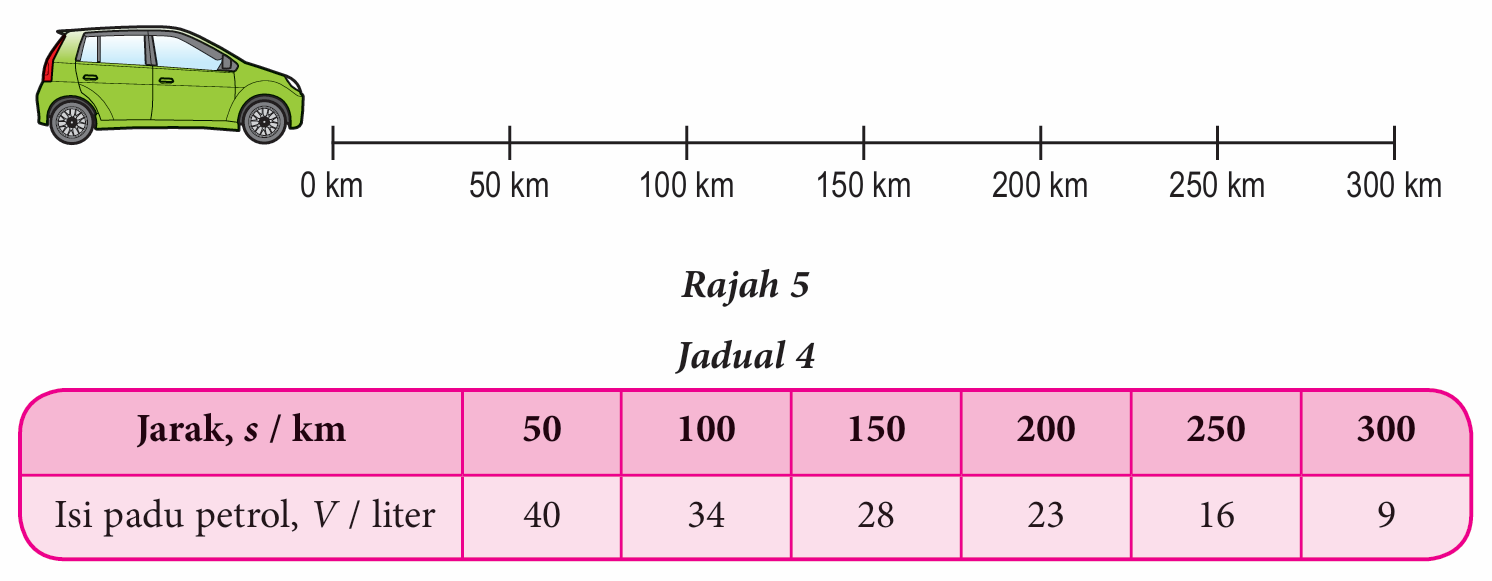
(a) Pemandu tersebut terlupa mencatatkan isi padu petrol pada titik permulaan perjalanan.
Bagaimanakah pemandu tersebut boleh menganggarkan nilai isi padu petrol keretanya pada permulaan perjalanan?
(b) Tentukan penggunaan isi padu petrol oleh enjin kereta tersebut bagi 80 km pertama.
Tunjukkan kaedah anda dengan terperinci.
(c) Jika penggunaan isi padu petrol enjin kereta bagi setiap 50 km dapat dijimatkan sebanyak 10%, tunjukkan nilai-nilai baharu V dan s dalam sebuah jadual.
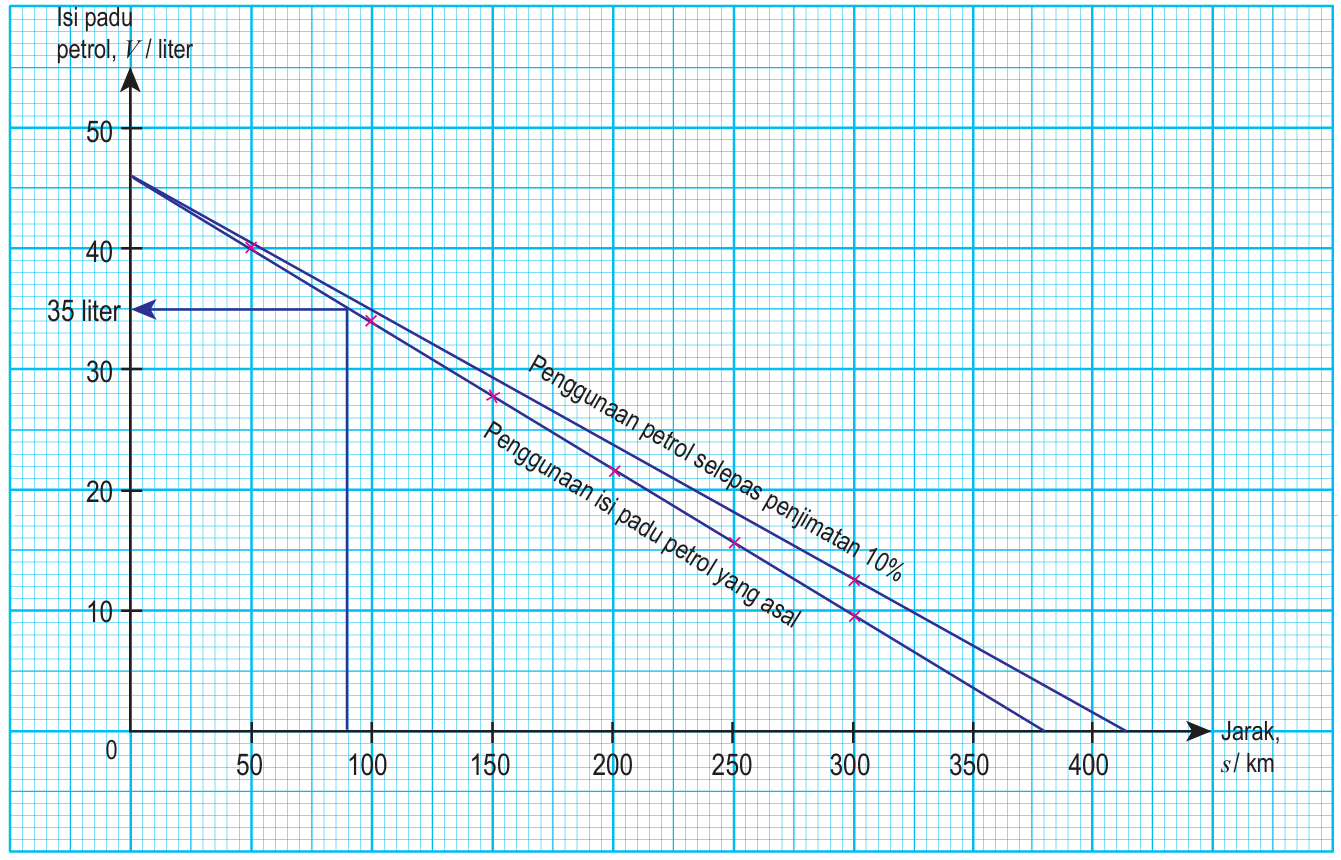
(d) Lukiskan graf V melawan s yang baharu.
Jawapan:
(a) Lukiskan graf V melawan s dan ekstrapolasi graf ke jarak s = 0 km, V = 46 liter
(b) – Lukiskan garis interpolasi pada s = 80 km, baca nilai V = 35 liter
– Penggunaan petrol oleh enjin pada 80 km pertama ialah (46 – 35) liter = 11 liter
(c)

(d)
Seorang pemandu ingin tahu penggunaan petrol oleh enjin kereta bagi setiap 1 km untuk perjalanan sejauh 300 km pada kelajuan malar. Beliau memasang alat pengukur isi padu petrol dalam keretanya untuk mencatatkan bacaan baki isi padu petrol pada setiap jarak 50 km dari titik permulaan. Jadual 4 menunjukkan bacaan-bacaan yang diperolehnya.

(a) Pemandu tersebut terlupa mencatatkan isi padu petrol pada titik permulaan perjalanan.
Bagaimanakah pemandu tersebut boleh menganggarkan nilai isi padu petrol keretanya pada permulaan perjalanan?
(b) Tentukan penggunaan isi padu petrol oleh enjin kereta tersebut bagi 80 km pertama.
Tunjukkan kaedah anda dengan terperinci.
(c) Jika penggunaan isi padu petrol enjin kereta bagi setiap 50 km dapat dijimatkan sebanyak 10%, tunjukkan nilai-nilai baharu V dan s dalam sebuah jadual.
(d) Lukiskan graf V melawan s yang baharu.
Jawapan:
(a) Lukiskan graf V melawan s dan ekstrapolasi graf ke jarak s = 0 km, V = 46 liter
(b) – Lukiskan garis interpolasi pada s = 80 km, baca nilai V = 35 liter
– Penggunaan petrol oleh enjin pada 80 km pertama ialah (46 – 35) liter = 11 liter
(c)

(d)


